Projects - Aerodynamic Decelerator Systems Laboratory
ADSC Projects
Precision Aerial Delivery
Snowflake: High-Precision Networked Micro-Light Aerial Delivery System
 The main objective of this research is the development of a prototype of a miniature precision airdrop system to evaluate some advanced concepts in controlling single and multiple (during mass airdrop) autonomously guided parafoils. These concepts include (but are not limited to) building a peer-to-peer networking frame with multiple ADS being its nodes, achieving a pinpoint accuracy for delivery of mission-critical payload, developing flocking and collision avoidance (deconfliction) capabilities, computing reachability sets to resupply troops at multiple locations in a timely manner, usage of unpowered and powered parafoils in urban warfare and exploring capabilities of a larger powered parafoil system to deliver and deploy smaller ones.
The main objective of this research is the development of a prototype of a miniature precision airdrop system to evaluate some advanced concepts in controlling single and multiple (during mass airdrop) autonomously guided parafoils. These concepts include (but are not limited to) building a peer-to-peer networking frame with multiple ADS being its nodes, achieving a pinpoint accuracy for delivery of mission-critical payload, developing flocking and collision avoidance (deconfliction) capabilities, computing reachability sets to resupply troops at multiple locations in a timely manner, usage of unpowered and powered parafoils in urban warfare and exploring capabilities of a larger powered parafoil system to deliver and deploy smaller ones.
Pegasus: Ultra-Light Guidance and Control System for Autonomous Parafoil
 This research addressed system identification and development of guidance, navigation and control system for an Ultra-Light autonomous high-glide-ratio parafoil-based delivery system.
This research addressed system identification and development of guidance, navigation and control system for an Ultra-Light autonomous high-glide-ratio parafoil-based delivery system.
AGAS: Affordable Guided Airdrop System
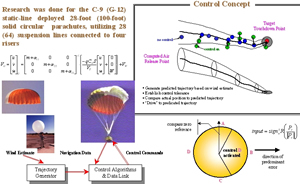 This research effort resulted in the development of autonomous guidance, navigation and control system for a flat solid circular parachute with added limited control authority. Such a system, known as Affordable Guided Airdrop System (AGAS), integrated a low-cost guidance and control system into a fielded cargo air delivery system.
This research effort resulted in the development of autonomous guidance, navigation and control system for a flat solid circular parachute with added limited control authority. Such a system, known as Affordable Guided Airdrop System (AGAS), integrated a low-cost guidance and control system into a fielded cargo air delivery system.
Other PADS-Related Developments
![]() The development of aerial payload delivery solutions continues. Current research exercises the legacy of the AGAS and Snowflake projects and explores several novel concepts
The development of aerial payload delivery solutions continues. Current research exercises the legacy of the AGAS and Snowflake projects and explores several novel concepts
Software
Video Scoring: Video Data Reduction and Air Delivery System Pose Estimation
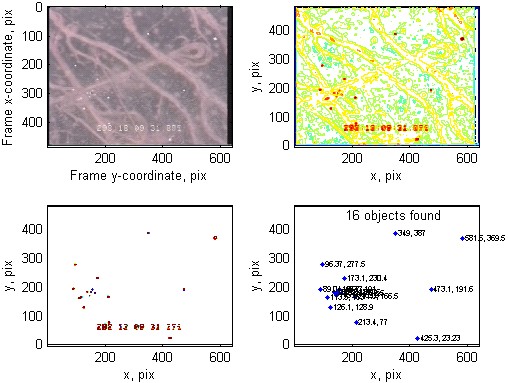
 This research addresses the problem of determining position and attitude of aerial delivery system (canopy and payload) based on observations obtained by several fixed cameras on the ground.
This research addresses the problem of determining position and attitude of aerial delivery system (canopy and payload) based on observations obtained by several fixed cameras on the ground.
Safety Fans GUI: Standalone Graphical Calculator for Safety Fans Prediction
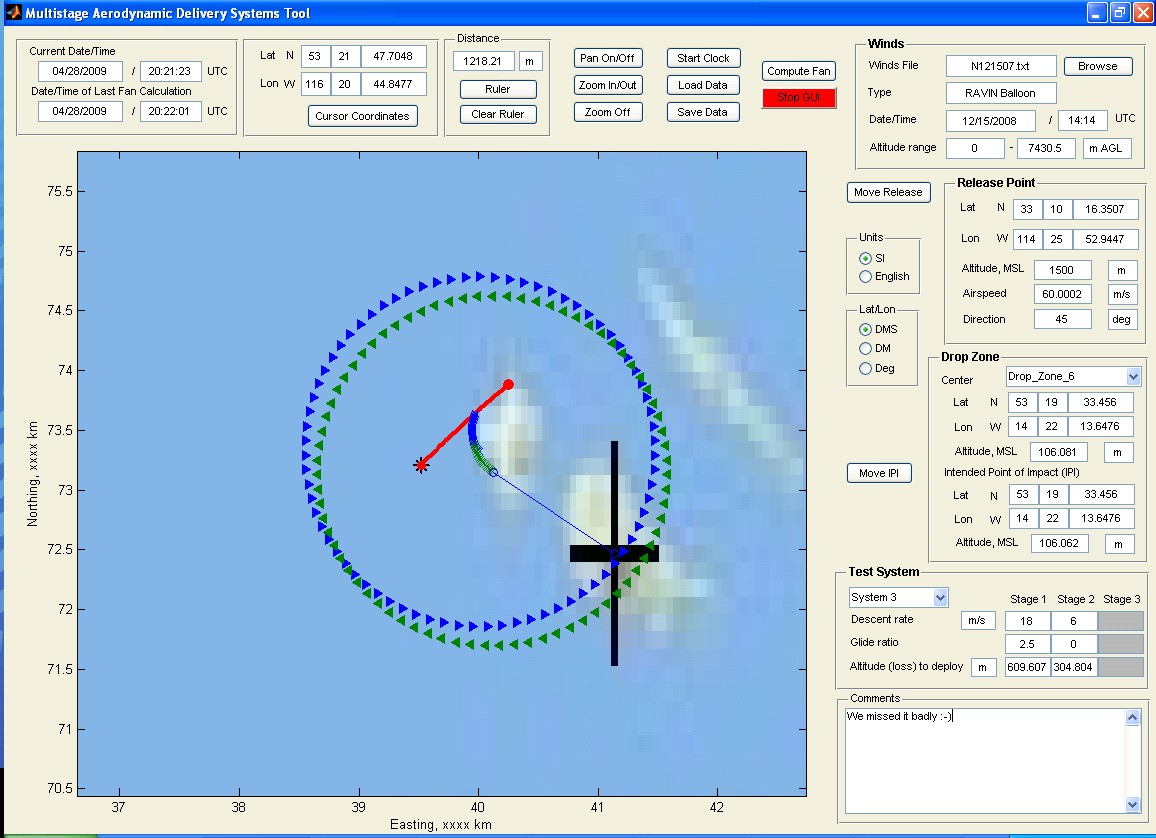 This project dealt with the development of mathematical foundation and practical algorithms to compute the safety fans to be used in conjunction with aerial payload delivery systems tests. It started from the development of the mathematical models to compute a descending/gliding trajectory for a generic multiple-stage system in the nominal (controlled) configuration and with a series of different failures (of canopy and controls).
This project dealt with the development of mathematical foundation and practical algorithms to compute the safety fans to be used in conjunction with aerial payload delivery systems tests. It started from the development of the mathematical models to compute a descending/gliding trajectory for a generic multiple-stage system in the nominal (controlled) configuration and with a series of different failures (of canopy and controls).
EO/IR Integration: Integrated Real-Time Image Processing System
This project pursued the development of an on-line monitoring system allowing to reliably extract certain features (the reference points) and new popping-up objects, that are needed to be related to the reference points, based on EO and IR video streams.
SimPADS: Virtual Simulation Environment
This research effort deals with creating integrated development environment for high-fidelity computer and hardware-in-the-loop simulations to conduct various studies in support of the actual airdrops. It is intended to significantly reduce the total number of the required tests and provide a tool for comparison of different GNC strategies applied to different-weight / different-dynamics aerial payload delivery systems.
Computer Vision Analysis of Test Items Dynamics
Algorithms developed within the Video Scoring and EO/IR Integration projects were adapted and enhanced to incorporate vision data in a variety of novel applications. Many of these applications dealt with tracking different test articles using standard and high-speed cameras and determining a pose of these objects based on video data.
Navaids: Feature-Based Navigation (page under construction)
Instrumentation
Sensor Fusion: Payload Derived Position and Attitude Acquisition System
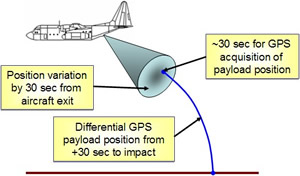 This research was fulfilled in parallel to the Video Scoring project. They both pursued the same goal of estimating the position and orientation of parachute recovery systems during the entire drop, from exiting an aircraft until impact, but using different sources of data.
This research was fulfilled in parallel to the Video Scoring project. They both pursued the same goal of estimating the position and orientation of parachute recovery systems during the entire drop, from exiting an aircraft until impact, but using different sources of data.
CAST-2000: GPS Constellation and Integrated INS/GPS Simulator
 This project aims at the development of cost-effective and efficient laboratory facility for thoroughly evaluating the capability of GPS-based integrated navigation systems, including aero delivery systems. The ability to test navigation system components, GPS receivers, IMU sensors, and software, constitutes a critical part of the research and development process. As the demand for GNSS products has increased, more receiver manufacturers and application developers have entered the market, GPS and GNSS simulators have become a bellwether for the GNSS industry, both mass market and professional.
This project aims at the development of cost-effective and efficient laboratory facility for thoroughly evaluating the capability of GPS-based integrated navigation systems, including aero delivery systems. The ability to test navigation system components, GPS receivers, IMU sensors, and software, constitutes a critical part of the research and development process. As the demand for GNSS products has increased, more receiver manufacturers and application developers have entered the market, GPS and GNSS simulators have become a bellwether for the GNSS industry, both mass market and professional.
RPT: Remotely Piloted Testbed for Persistant Surveillance
![]() The goal of this project was to develop a fleet of unmanned aerial systems (UAS) carrying a variety of sensors enabling persistent surveillance of different test activities from the air. Four different-size UAS were considered as a remotely piloted testbed (RPT) to support the aforementioned mission.
The goal of this project was to develop a fleet of unmanned aerial systems (UAS) carrying a variety of sensors enabling persistent surveillance of different test activities from the air. Four different-size UAS were considered as a remotely piloted testbed (RPT) to support the aforementioned mission.
Projects List
- Snowflake: High-Precision Networked Micro-Light Aerial Delivery System
- Pegasus: Ultra-Light Guidance and Control System for Autonomous Parafoil
- AGAS: Affordable Guided Airdrop System
- Other PADS-Related Developments
- Video Scoring: Video Data Reduction and Air Delivery System Pose Estimation
- Safety Fans GUI Standalone Graphical Calculator for Safety Fans Prediction
- EO/IR Integration: Integrated Real-Time Image Processing System
- SimPADS: Virtual Simulation Environment
- Computer Vision Analysis of Test Items Dynamics
- Sensor Fusion: Payload Derived Position and Attitude Acquisition System
- CAST-2000: GPS Constellation and Integrated INS/GPS Simulator
- RPT: Remotely Piloted Testbed for Persistant Surveillance